- cross-posted to:
- [email protected]
- cross-posted to:
- [email protected]
cross-posted from: https://lemmy.world/post/6080744
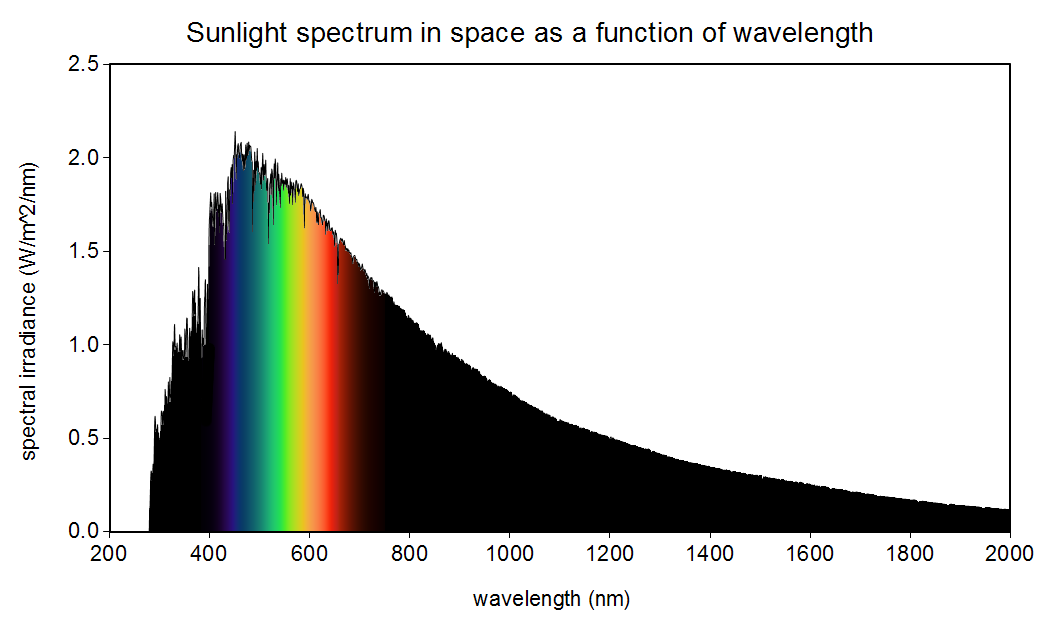
The sun is not yellow or orange as we see in books and movies. It emits all the colours in the visible spectrum (also in other spectrums as well) making it white!


So we can see the where this weirdness comes from when we look at the energy for a photon, E=hf=hc/λ
When we integrate we sort of slice the function in fixed intervals, what i called above df and dλ. So let’s see what is the difference in energy when our frequency interval is, for example, 1000 Hz, and use a concrete example with 100 Hz and 1100 Hz. Then ΔE = E(1100 Hz) - E(100 Hz) = h·(1100 Hz - 100 Hz) = h·(1000 Hz) = 6.626×10^-31 joules. You can check that this difference in energy will be the same if we had used any other frequencies as long as they had been 1000 Hz apart.
Now let’s do the same with a fixed interval in wavelength. We’ll use 1000 nm and start at 100 nm. Then ΔE = E(100 nm) - E(1100 nm) = hc·(1/(100 nm)-1/(1100 nm)) = 1.806×10^-18 joules. This energy corresponds to a frequency interval of 2.725×10^15 hertz. Now let’s do one more step. ΔE = E(1100 nm) - E(2100 nm) = 8.599×10^-20 joules, which corresponds to a frequency interval of 1.298×10^14 hertz.
So the energy emitted in a fixed frequency interval is not comparable to the energy emitted in a wavelength interval. To account for this the very function that is being integrated has to be different, as in the end what’s relevant is the result of the integral: the total energy radiated. This result has to be the same independent of the variable we use to integrate. That’s why the peaks in frequency are different to those in wavelength: the peaks depend on the function, and the functions aren’t the same.