The US FCC defines ionizing radiation as wavelengths smaller than 124 nm (which corresponds more or less to the ionization energy of both oxygen and hydrogen, so it is a sensible definition).
The “most starlight” part is a bit trickier. Stars emit light in a wide spectrum (approximately black body radiation) depending on their temperature: hotter stars emit bluer light and are more luminous, but very rare, while cooler stars are redder and fainter, and much more common. Yellow stars (spectral type G), like the Sun, emit mostly between 400 nm and 750 nm (visible spectrum), while red stars (spectral type M) mostly emit from 700 nm to 1000 nm,
So let’s say that you want all the light with wavelengths of 1000 nm or smaller turned into ionizing radiation. That gives us a blue-shift of 1+z = lambda_obs/lambda_em = 124 nm/ 1000 nm = 0.124.
The relation between speed and blue(/red)-shift is given by the relativistic Doppler effect:
1+z = sqrt((1+beta)/(1-beta))
where beta=v/c and c is the speed of light. Solving for beta
beta = ((1+z)^2 -1)/((1+z)^2 +1)
And plugging the numbers, you get beta = -0.970, where the minus sign means that you are moving towards the star. At 97% of the speed of light.
If you only wanted to turn most of the sunlight into ionizing radiation, you would need “just” 94.7% of the speed of light.
This is a fantastic answer that clearly spells out the assumptions made and the effects of those assumptions. Well done :)
The sci fi fan in me now wonders: assuming you get to 0.95c before it becomes truly problematic, what kind of shielding would you need at the front of your probe(/spacecraft/etc.) to prevent the effect from totally destroying the probe. Like you can’t just blast electronics with x-rays and harsher and expect it to run. So there is probably a mass tradeoff here with a big ole block of ablating lead at the front that ablates from radiation spalling?
There’s probably a cost optimization curve there – mass of shielding, travel time, energy cost to accelerate the probe.
Furthermore, there would be a pressure exerted by that radiation that should slow the probe down over time, but the rate of slowing will depend on the mass/cross section/etc.
And of course running into an interstellar proton or such will be somewhat of a high energy event… More shielding, or hypothetical defenses like the bussard ramscoop…
A couple non-quantitative thoughts on this:
-
Space is big and empty. In order to have significant amounts of radiation energy hitting you you’d have to be going quite close to stars thanks to the cube energy drop-off.
-
Space probes do have this kind of shielding on their chips! They also use multiple independent identical processors that vote on results as it’s unlikely for a high energy particle to scramble a majority of the chips in an identical way. This is also why space tech tends to use old manufacturing nodes that have huge (by earth bound comparison) transistors.
Good points.
I wonder what the dose would look like to a square metre, framed in human reference terms. Better or worse than medical imaging. That would require figuring out photon flux, above 750nm. But there is also relativistic cross section changes happening, so does that affect the flux?
I’m reminded of a first year physics prof that suggested we figure out how fast we’d need to go to fit through the head of a needle (in a vacuum).
The redundant computing this is a fantastic invention. I’m aware that SpaceX is using off-the-shelf computers for this instead of the longstanding tradition to use only “rad hardened hardware”, preferring to rely on multiple redundancy for weight and cost savings. Without knowing the flux at 0.95c though, it’d be hard to estimate how well the strategy would work :)
-
Should be impossible due to the universe being homogeneous. I.e. you can’t face all the ligh and move toward it at once since it come for all directions at once.
You can just math out when visible light would be shifted to a specific wavelength in your direction of travel.
Minor caveat: If you exploded yourself you might be able to go every direction at once. But not in one piece, I guess.
EDIT: Ah! After sending this answer I saw jorge’s answer!! So this answer is redundant, but at least you can see that two people arrived at virtually the same conclusion 😀
We need to define a threshold of energy that we consider “ionizing radiation”, and we also need to a more precise definition of “starlight”.
I will arbitrarily select the ionizing radiation threshold to be at 10 eV (124 nm). As for “starlight”, let’s just say that we want to push the 750 nm red light all the way until the point where it becomes ionizing. One thing to consider is that in this situation you will also push infra-red light from the stars towards the visible, so if a star emits a lot infrared this IR light will become “starlight”. So the answer can be muddled up by all of these definitions as well as the emission properties of the star.
To keep it simple… Let’s shift 750 nm red light to 124 nm ionizing radiation. You can rearrange the Doppler expression from this website to solve for the “v” to get the velocity needed to transform 750 nm to 124 nm. The solution I get is -284,035,329 m/s, with the “-” sign indicating movement of the receiver towards the source.
You can double-check by inputting 750 nm as the wavelength from the light emitted by the source, -284,035,329 m/s as the velocity, and the speed of light as “c”:
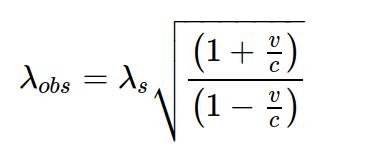
Then, if you agree with the assumptions, definitions, and the analysis, the receiver needs to move at about 94.68% the speed of light to shift the redder starlight into the ionizing radiation range.
Much thanks! Was coming at it from a sci fi perspective, so definitions are laymans definitions, and you’ve made good assumptions. It also lines up nicely with the other answers :)
In conclusion, it’ll become a massive problem for a probe at 0.95c ish.
5%
A question arising from my love of hard sci fi. Hoping there are relativity specialists about :)
deleted by creator